算法

关于深度优先搜索的一点小心得

Posted by SpirytusZ on 2018-10-18

1. 前言

上周刷了20来道LeetCode的题，总结出了一些关于深度优先搜索的小小的心得，于是有了这篇博客。这次的总体思路是：

  1. 深度优先搜索算法的工作过程
  2. 如何使用深度优先搜索算法来进行遍历
  3. 两个有趣的问题
  4. 深度优先搜索算法和循环的关系

那我们开始吧。

2. 深度优先搜索

深度优先搜索（Deep First Search, DFS）是一种先序遍历，先遇到的节点先访问，然后以这个节点为起点，继续向下遍历，直至所有的节点都被访问（连通分量 == 1的情况下）。所以，个人认为，DFS可以看做是一种暴力枚举的算法。多说无益，下面一个例子可能会让你对DFS有初步的了解。

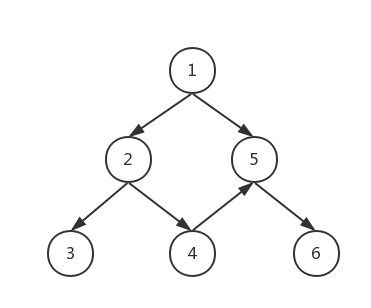
这是一个有向、无环、连通分量为1的图，我们可以用邻接矩阵来存储它：

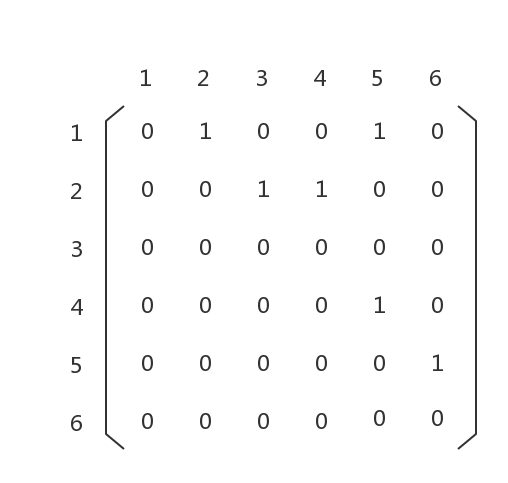
这个矩阵的意义是，如果graph[i][j] == 1，那么节点i和节点j的关系是i -> j，即有从节点i到节点j的通路。
我先不放代码，我先跟着DFS的思路来对上面的图，以节点1为起点深度优先遍历一次。
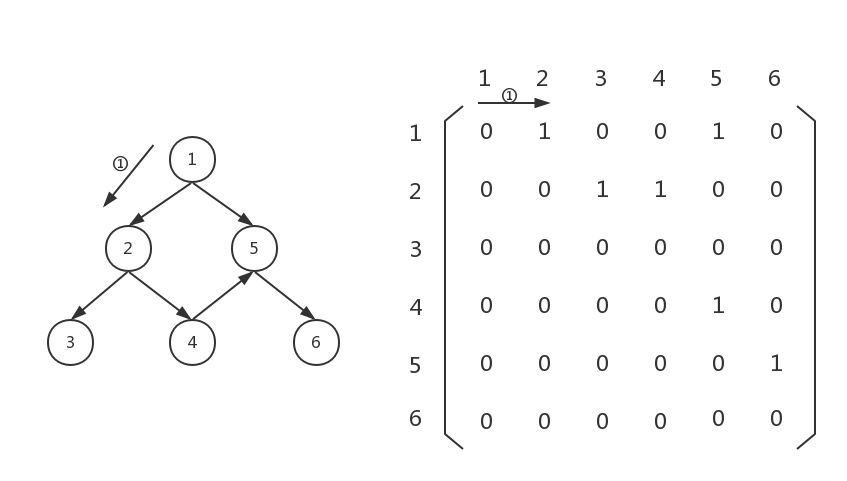
由于是从节点1开始遍历，因此我们先看看数组graph[0][0…5]，从0到5扫一遍，发现graph[0][1]不为零，说明有节点1到节点2的边。由于DFS是先访问，再以此节点为起点继续向下遍历，所以我们先把节点1，节点2存起来，然后以节点2为起点，向下遍历，如下图：

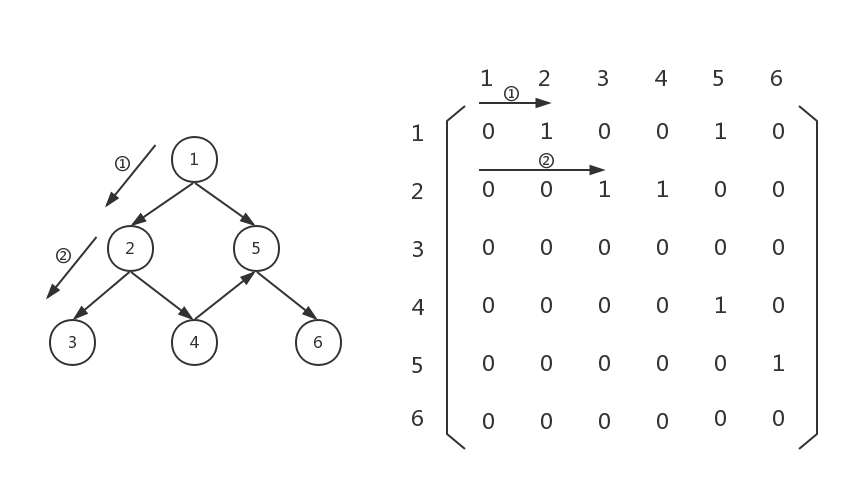
接下来，扫一遍graph[1][0...5]，发现graph[1][2]不为0，说明节点2连向节点3，则把节点3存起来，然后以节点3为起点，向下遍历：

很好，接下来扫一遍graph[2][0...5]，但是遗憾的是，数组graph[2][0...5]并没有值为1的元素，这表明，节点3没有连向其他节点，即出度为0。因此，这时候需要回溯，回到上一层：

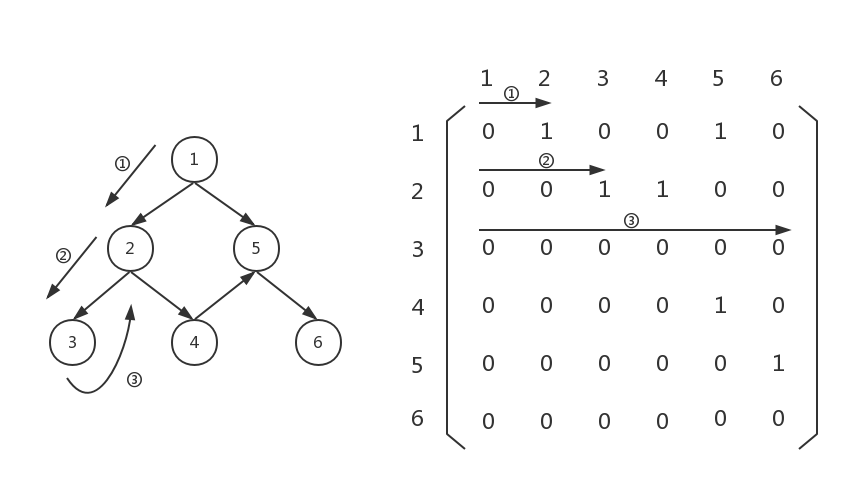
这时，上一步已经回溯到了上一层，此时我们需要扫描graph[1][3...5]，此时发现graph[1][3]不为0，说明节点2连向节点4，那么应该把节点4存起来，接下来以节点4为起点继续向下遍历：

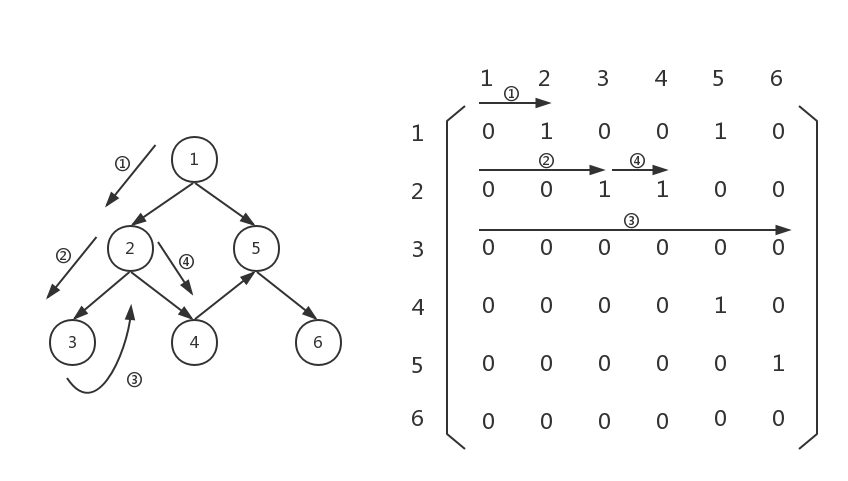
很好，接下来扫一遍graph[3][0...5]，发现graph[3][4]不为0，说明节点4连向节点5，我们应该把节点5存起来，然后以节点5为起点，向下遍历：

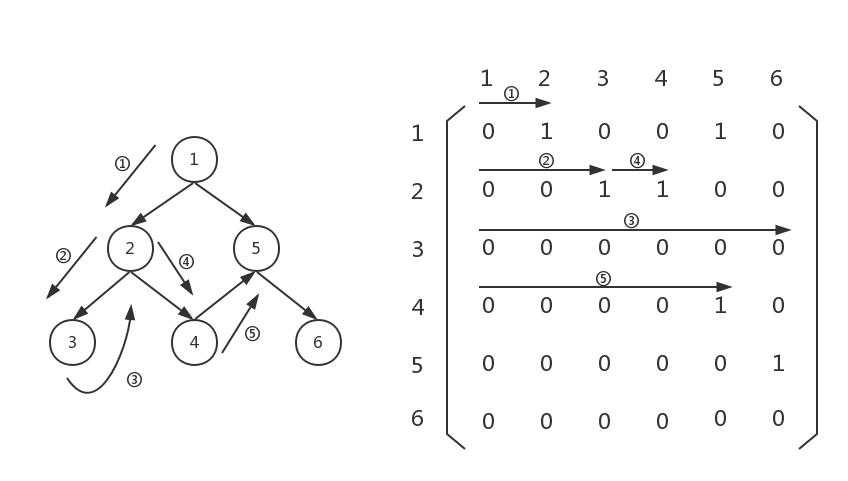
此时，我们需要扫描一遍graph[4][0...5]，发现graph[4][5]不为0，说明节点5连向节点6，我们应该把节点6存起来。然后以节点6位节点，向下遍历：

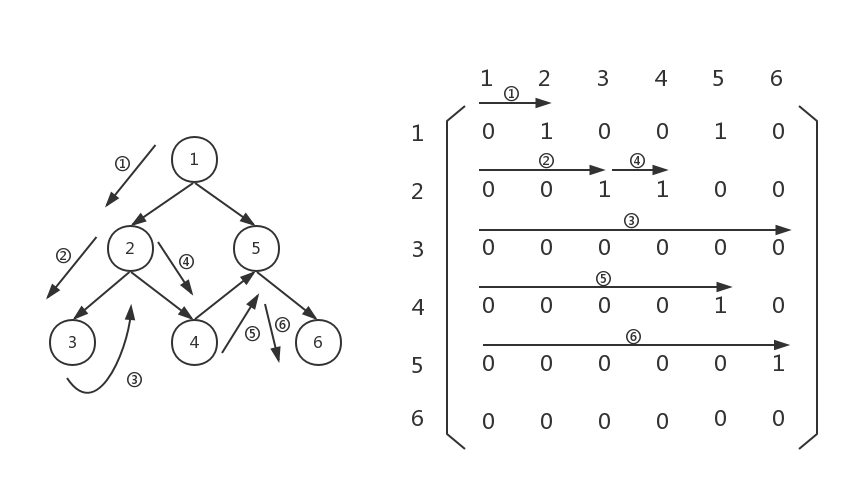
然而，graph[5][0...5]并没有不为0的元素，这说明，节点6的出度为0，应该回溯，回到上一层：

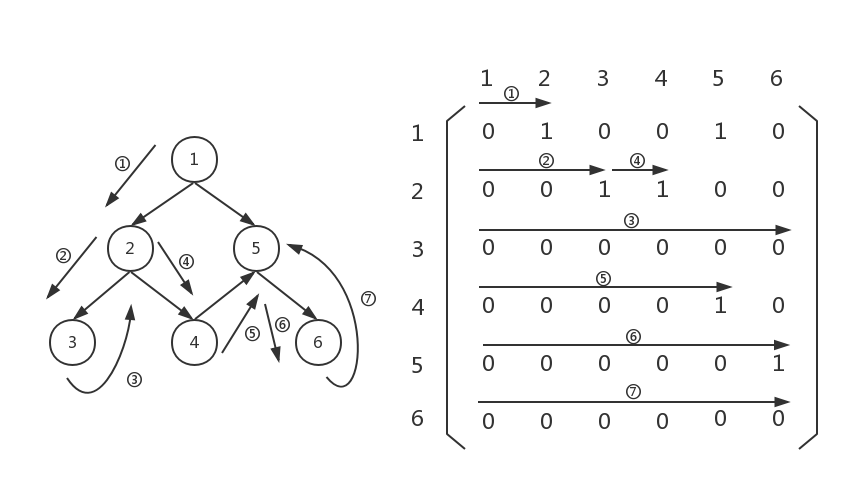
此时，我们回到了graph[4][0...5]，但是graph[4][0...5]已经扫完了，我们继续回溯，回到graph[4][0...5]的上一层graph[3][5...5]，但是graph[3][5...5]已经没有不为0的元素了，所以我们继续回溯，回到上一层：

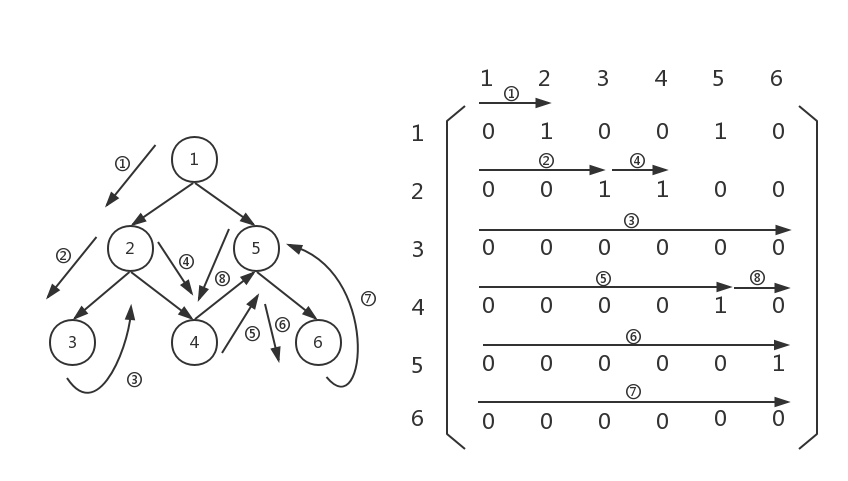
此时，我们回到了graph[1][4...5]，graph[1][4...5]已经没有不为0的元素了，继续回溯，回到上一层：

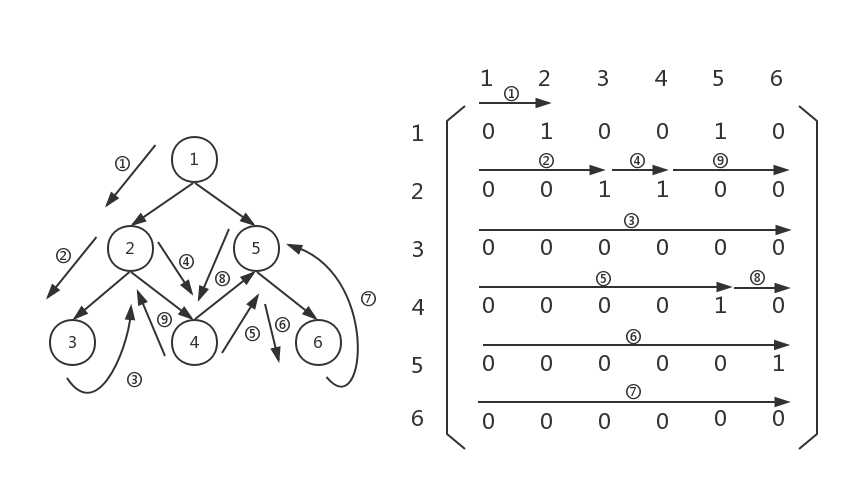
终于回到graph[0][2...5]了，我们继续扫描，发现graph[0][4]不为0，但是节点5（graph[0][4]的4表示节点5）已经访问过了，我们没必要，也不能继续存节点5了，所以我们忽略graph[0][4]，继续扫描，最后扫描完毕，遍历结束。

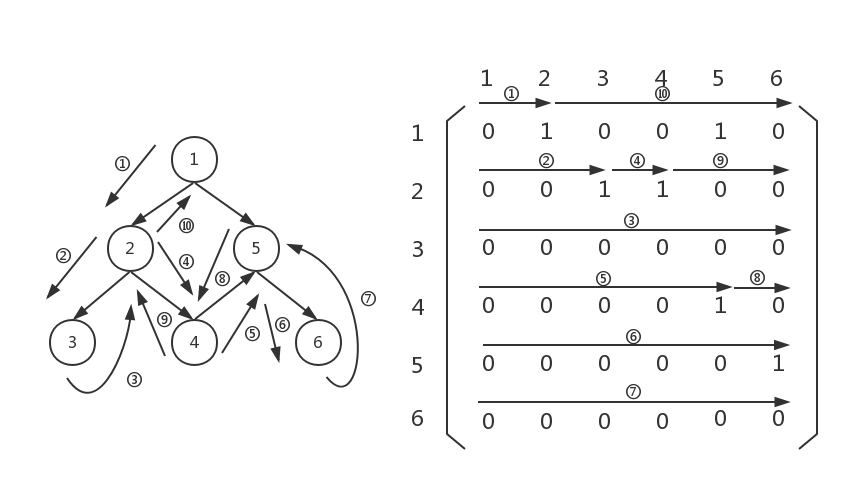
这个过程如果明白了，代码就很容易写出来：

1
2
3
4
5
6
7
8
9
10
11
private static void deepFirstSearch(int[][] graph, List<Integer> result, int[] accessFlag, int startVertex) {
    if (startVertex < graph.length) {
        result.add(startVertex + 1);
        accessFlag[startVertex] = 1;
        for (int i = 0; i < graph[startVertex].length; i++) {
            if (graph[startVertex][i] == 1 && accessFlag[i] != 1) {
                deepFirstSearch(graph, result, accessFlag, i);
            }
        }
    }
}

解释一下，for循环对应上面所说的扫描，startVertex是当前的起点。如果graph[startVertex][i]不为0，说明有从startVertex到i的通路，即startVertex -> i，并且如果节点i并未被访问（访问节点i时accessFlag[i]会被置为1），那就以节点i为起点向下遍历；而if语句是为了检查输入数据是否合法。
方法已经写好，我们只需要如下调用，就能拿到DFS的结果：

1
2
List<Integer> result = new ArrayList<>();
deepFirstSearch(graph, result, new int[graph.length], 0);

总结一下，DFS就是先遇到先访问，再以此为起点继续访问，直至全部访问完毕，很像先序遍历。

3. DFS应该怎么用来遍历？

通过上面的说明，想必已经对DFS有初步的理解了吧。那我们继续吧。
前面我已经说过，DFS可以看做是一种暴力枚举算法。结合上面的例子，我们可以看到，邻接矩阵graph的所有元素都被DFS算法扫描了一遍，所以至少从这个例子来看DFS是一种暴力枚举算法。我认为确实也是。
OK，既然我们已经知道DFS可以看做一种暴力枚举算法，我们应该怎么用它来枚举？在这里，我想通过分析二叉树的先序遍历过程乃至多叉树的遍历过程，进而推广到一般的情况来说明。

首先定义一下树的数据结构：

1
2
3
4
5
private class Tree {
    int data;
    Tree leftChild;
    Tree rightChild;
}

自然地，该二叉树的先序遍历就可以这么写：

1
2
3
4
5
6
7
private static void preOrderTraversal(Tree parent) {
    if(tree != null) {
        accessTreeVertex(parent);
        preOrderTraversal(parent.leftChild);
        preOrderTraversal(parent.rightChild);
    }
}

二叉树的遍历如何推广到多叉树的遍历？如果可以用for循环将这个节点的所有孩子节点列举出来那就好了。确实可以。我们只需要稍微改写一下数据结构：

1
2
3
4
private class Tree {
    int data;
    Tree children[];
}

然后如下遍历：

1
2
3
4
5
6
7
8
private static void preOrderTraversal(Tree parent) {
    if(tree != null) {
        accessTreeVertex(parent);
        for (int i = 0; i < parent.children.length; i++) {
            preOrderTraversal(tree.children[i]);
        }
    }
}

为什么要这么写，这段代码背后的思路是什么？
如果children.length == 2那就是二叉树的情形。自然地，如果children.length为任意值，那就是任意多叉树的情形，即可以对任意多叉树进行遍历。其实思路就是将孩子节点转化成可以被for循环列举的形式（如上面是把孩子节点转成数组）。
现在，我们看看多叉树的子结构：

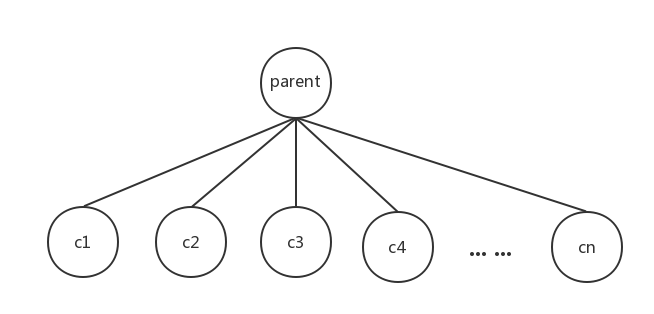
这个多叉树的子结构，是一个父节点带着n个子节点(n是任意一个大于0的整数)的结构。我们如何对这个子结构进行遍历？

  1. 首先我们访问父节点，即accessVertex(parent)
  2. 因为父节点有n个子节点，所以我们挨个的访问它们。由于孩子节点存在数组中，于是我们可以用for循环解决。

因此遍历一个子结构就可以这么写：

1
2
3
4
5
6
7
8
9
// traversal the substructure of tree
// Input: SubStructure of tree

function traversalSubStructure(Tree subTreeRoot):
    access(subTreeRoot)
    for i in 0 to subTreeRoot.children.length
        traversalSubStructure(subTreeRoot.children[i])
    end
end

由于多叉树所有的子结构共同组成整个多叉树（即可以被递归定义），所以我们可以用递归来完成遍历。
如何使用递归？只需要确认好边界条件即可。初始条件当然是放入一个树的根，停止向下递归则是遇到了叶子节点，即这个节点的children域为空。所以：

1
2
3
4
5
6
7
8
9
10
11
// Traversal tree
// Input: root of tree

function traversalTree(Tree treeRoot):
    if treeRoot not null then
        access(treeRoot)
        for i in 0 to treeRoot.children.length
            traversalSubStructure(treeRoot.children[i])
        end
    end
end

说了那么多，我想表达的是：如果一个节点，它的子节点可以用循环来列举的话，那我们可以用循环+递归的形式来进行遍历这个图。
更近一步来说，我们可以用递归+一个for循环来实现n重循环，进而进行遍历。n重循环天生就适合拿来作为枚举的工具。所以，我们可以把问题写成n重循环的形式，然后再转化成递归，就可以用DFS来解决遍历问题。
因此，DFS可以写成如下形式：

1
2
3
4
5
6
7
void DFS(Graph graph) {
    if(边界条件) {
        for(i;循环条件;i++) {
        	DFS(graph.child.get(i));
        }
    }
}

4. 两个问题

在刷题的过程中，我遇到了两个很有意思的问题，都可以用DFS来解决，这里分享一下，分别是迷宫问题和不重复字符的字符串。

4.1. 迷宫问题

长话短说，迷宫问题是这么被描述的（LeetCode上的描述很长，我就不贴了）：
给定一个二维数组来表示一个迷宫。这个数组里的元素要么为0要么为1；0代表可以通过，1代表是墙壁，不可通过。
比如说，给定一个二维数组：

1
2
3
4
5
6
7
8
int[][] maze = {
    {1, 0, 0, 0, 0, 1},
    {1, 1, 1, 1, 1, 1},
    {0, 1, 0, 1, 1, 0},
    {0, 1, 0, 0, 1, 0},
    {1, 1, 1, 0, 1, 1},
    {0, 0, 1, 1, 1, 0}
};

它表示这个迷宫，灰色为墙壁，白色为通路：

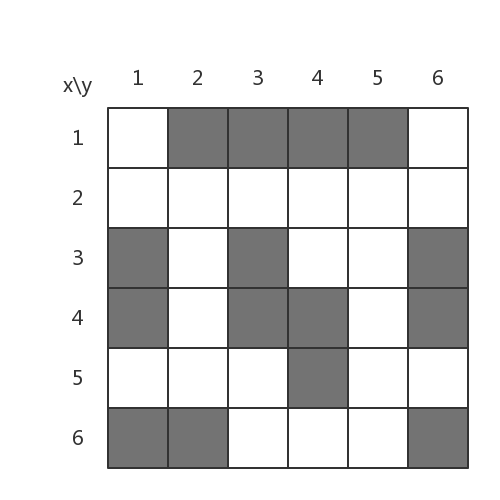
现在，给定一个起点和终点，找出一条可行的路径来走出这个迷宫。

不妨以上图为例子，起点为(1, 1)，终点为(6, 5)。

如何用DFS的实现来解决迷宫问题？我们走到一个点时（必然的，这个点的值为0，即为通路），我们可以选择向上、向下、向左或者是向右走；而前面的问题，都是一个父节点带着n个子节点的情形，我们可以照葫芦画瓢，父节点就是当前节点，而子节点就是上、下、左以及右的节点，画成图的话是这样的：

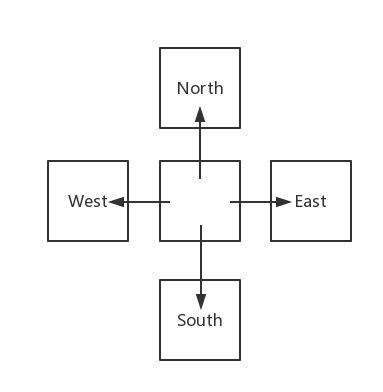
先对这个子结构进行遍历，伪代码：

1
2
3
4
5
6
7
8
// Traversal currentPoint and its North, South, West and East Point
// Input: maze, currentPoint

function traversalCurrentPoint(Maze maze, Point currentPoint):
    for point in {currentPoint.North, currentPoint.South, currentPoint.West, currentPoint.East} :
        traversalCurrentPoint(point)
    end
end

接下来确定好边界条件，初始条件当然是给一个起点，停止向下递归的条件是：

  1. 遇上墙壁
  2. 遇上终点

所以，对每个子结构遍历的伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Solve Maze Problem
// Input: maze, start, end

function solveMaze(Maze maze, Point start, Point end, Result result):
    if start == end then 
        result.add(start)
        return
    else if is not wall then 
        result.add(start)
        for Point in {start.North, start.South, start.West, start.East} :
            solveMaze(maze, start, end, result)
        result.remove(start)
    end
end

因此，相应的Java代码实现有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
private static Point[] getPoints(Point currentPoint) {
    int currentX = currentPoint.x;
    int currentY = currentPoint.y;
    return new Point[]{
            new Point(currentX - 1, currentY), // North
            new Point(currentX + 1, currentY), // South
            new Point(currentX, currentY - 1), // West
            new Point(currentX, currentY + 1)  // East
    };
}

private static boolean solveMaze(int[][] maze, List<Point> result, Point start, Point end) {
    int x = start.x;
    int y = start.y;
    if (x == end.x && y == end.y) {
        result.add(start);
        return true;
    } else {
        result.add(start);
        Point[] points = getPoints(start);
        for (int i = 0; i < points.length; i++) {
            if (isValidPoint(maze, points[i])
                   && hasNotAccess(result, points[i])
                   && solveMaze(maze, result, points[i], end)) {
                return true;
            }
        }
        result.remove(start);
    }
    return false;
}

其中isValidPoint()会判断是否越界或者遇上墙壁；而hasNotAccess()会判断节点是否被访问过，这么做可以防止North -> South -> North ...或者East -> West -> East ...的死循环。

代码的思路就是把所有子节点转换成可以被for循环枚举，每走一步，以当前节点为父节点继续枚举（即向下遍历），直到遇到终点或者墙壁后回溯。其实，这段DFS代码的可以转换成一个n重循环。

4.2. 不重复的字符的字符串

其实这题不是LeetCode上的，是我从同学那里听说的。听完题目之后觉得挺有意思的，觉得用DFS可解，然后码了下代码，发现真的可以。
这道题是这么描述的：

给定一个没有重复字符的字符串s，字符串的第i个字符用si表示，即s = s1s2s3…si…sn
请给出k个不重复的，由s[1…n]组成的，没有重复字符，长度为n的字符串。
Example 1:
    Input:
        s = “01234567”, k = 3
    Output:
        ”01234567”, “74625310”, “45367201”

Example 2:
    Input:
        s =”abc”, k = 5
    Output:
        ”abc”, “bca”, “cba”, “acb”, “bac”

给定的字符串s是一维的，明显不能直接用DFS来搜索。能使用DFS，数据必须是二维的。于是我们可以构造一个矩阵，矩阵就是二维的，以s = “abcd”为例，如下：

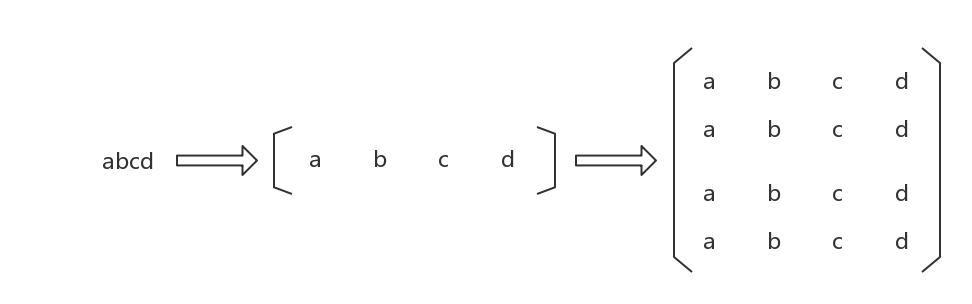
为什么我会想到构造一个矩阵出来？原因不难理解。前面我不断的说：DFS代码可以转换成一个n重循环。n重循环很好枚举，所以我就构造出一个4*4的矩阵，每一行都是s
这样我就能写成如下形式：

1
2
3
4
5
6
7
8
9
for i in 0 ~ 3:
    for j in 0 ~ 3: 
        for m in 0 ~ 3: 
            for n in 0 ~ 3: 
                rs = s[i] + s[j] + s[m] + s[n]
            end
        end
    end
end

然后我就可以转成递归的形式：

1
2
3
for i in 0 ~ 3: 
    DFS(s, i)
end

转换成递归形式，可能就就不大容易看懂了，我们来看看这张图：

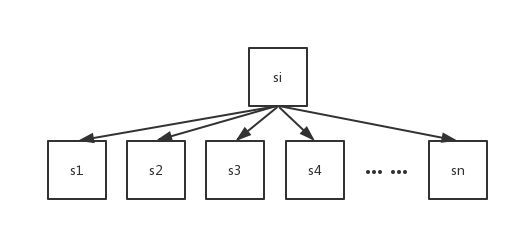
当我们走到了第i个字符串时，接下来该往s1...sn走，于是我们可以用循环来枚举。

所以，相应的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private static void bruteSearch(String[] targetCharMatrix, StringBuilder stringBuilder, List<String> result, int[] accessFlag, int depth) {
    if (depth < targetCharMatrix.length) {
        for (int i = 0; i < targetCharMatrix[depth].length(); i++) {
            if (accessFlag[i] != 1) {
                stringBuilder.append(targetCharMatrix[depth].charAt(i));
                accessFlag[i] = 1;
                bruteSearch(targetCharMatrix, stringBuilder, result, accessFlag, depth + 1);
                accessFlag[i] = 0;
                stringBuilder.deleteCharAt(stringBuilder.length() - 1);
            }
        }
    } else {
        result.add(stringBuilder.toString());
    }
}

先解释一下参数列表：
其中targetCharMatrix是根据s构造出来的矩阵；
stringBuilder是用来拼接字符的对象；
result是用来存放结果的对象；
accessFlag是存放访问结果，如果第i个元素为0则表示第i个字符还没被访问（拼接），否则如果为1则表明已经被访问（拼接）过；
depth表示已经拼接字符的个数。

然后就是方法体：
首先判断是否超过最大深度，即depth是否等于4。
如果小于4：那就遍历targetCharMatrix[depth][0...3]。如果targetCharMatrix[depth][i]没被访问过，那就把accessFlag[i]置1，然后用stringBuilder把targetCharMatrix[depth][i]拼接进来，然后向下遍历，直至回溯回来后，将访问标志accessFlag[i]置0，把targetCharMatrix[depth][i]从stringBuilder中移除。

否则，如果depth等于4：说明此时stringBuilder.length() == 4，那就把它加到结果result里就ok了。其实还是一个n重循环问题。

其实，直接传一个矩阵(String[] targetCharMatrix)没有必要，因为这个矩阵的每行都一样。我们只需要传一个原字符串(即矩阵的任意一行)，再用depth来控制最大深度(矩阵的行数)就可以了。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private static void bruteSearch(String targetChar, StringBuilder stringBuilder, List<String> result, int[] accessFlag, int depth) {
    if (depth > 0) {
        for (int i = 0; i < targetChar.length(); i++) {
            if (accessFlag[i] != 1) {
                stringBuilder.append(targetChar.charAt(i));
                accessFlag[i] = 1;
                bruteSearch(targetChar, stringBuilder, result, accessFlag, depth - 1);
                accessFlag[i] = 0;
                stringBuilder.deleteCharAt(stringBuilder.length() - 1);
            }
        }
    } else {
        result.add(stringBuilder.toString());
    }
}

5. 由两个问题所引发的思考

上面已经解释了，DFS可以写成n重循环的形式。所以DFS和n重循环有什么关系？
DFS的基本形式，就是一个循环内调用自身。即一个循环+递归的形式：

1
2
3
4
5
6
7
8
function DFS(graph, depth):
    if depth < maxDepth then
        for i in 0 ~ graph.get(depth).length():
            access(graph, depth)
            DFS(graph, depth + 1)
        end
    end
end

如果graph是4*4的，如果调用DFS(graph, 0)，
那么第一层：

1
2
3
4
5
6
for i in 0 ~ 3:
    if 0 < 4 then
        access(graph, 0)
        DFS(graph, 0 + 1)
        end
end

第二层：

1
2
3
4
5
6
for i in 0 ~ 3:
    if 1 < 4 then
        access(graph, 1)
        DFS(graph, 1 + 1)
        end
end

第三层：

1
2
3
4
5
6
for i in 0 ~ 3:
    if 2 < 4 then
        access(graph, 2)
        DFS(graph, 2 + 1)
    end
end

第四层：

1
2
3
4
5
6
for i in 0 ~ 3:
    if 3 < 4 then
        access(graph, 3)
        DFS(graph, 3 + 1)
    end
end

把第i层的DFS(graph, (i - 1) + 1)替换成第i + 1层的代码，可以得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for i in 0 ~ 3:
    if 0 < 4 then
        access(graph, 0)
        for i in 0 ~ 3:
            if 1 < 4 then
                access(graph, 1)
                for i in 0 ~ 3:
                    if 2 < 4 then
                        access(graph, 2)
                        for i in 0 ~ 3:
                            if 3 < 4 then
                                access(graph, 3)
                                DFS(graph, 3 + 1)
                            end
                        end
                    end
                end
            end
        end
    end
end

从上面可以看出，DFS本质就是一个n重循环，DFS自然可以用n重循环来表示。

其实，观察每一层，每一层不一样的地方也就只有传的参数的值不同，也能看出这就是一个n重循环，有点像数学归纳法的递推。
还有就是，我上面不断的提子结构，其实我个人觉得能写成递归解决的问题，都很像数学中的分形。

6. 总结

  1. 如果一个枚举问题，它的子结构共同组成该问题，就像上面提到的迷宫问题一样，每走一步后，可以上下左右走，这是一个子结构，共同组成原问题，那么这个问题就可以写成n重循环的形式。既然能够写成n重循环的形式，自然就能转化成递归的形式，就能用DFS的思想解决。
  2. 如果一个枚举问题，它的子结构不能组成该问题，那我们就可以转化一下，如果能转化成让它可以由子结构组成，就像上面提到的不重复字符的字符串一样，一维的字符串自然没有子结构能够组成这个问题，那我们就构造一个矩阵，这样我们就能在递归深度为depth时，访问第1，第2 … 第n个元素，写成n重循环的形式，从而转化成递归进而用DFS的实现解决。
  3. DFS是解决枚举问题的基础，但不是所有问题都能照搬DFS的代码得到解决，需要具体情况具体分析。

7. 感想

在这之前，我对DFS的理解，也仅仅只是对二叉树的遍历。刷了一定量的题，我慢慢发现，只要给初始条件和停止条件，递归可以解决需要多重循环的问题，也就是DFS的实现。所以刷题还是有用的！想要对算法有理解还是要多刷题(不会可以看看Discussion，里面各路大神各种骚操作，都能解决问题)。就这样吧。如果本文有什么问题，请指教，共同进步，谢谢~！