快速排序不快了？重复元素下的快速排序

前言

快速排序，就像它的名字一样，它做排序很快，空间复杂度O(1)下，它的平均时间复杂度为O(nlog₂n)。但是在某些情况下，快速排序不快了，表现出来的性能和冒泡排序排序这类时间复杂度为O(n²)相差无几。因此，本文将解决：

• 快速排序的工作原理
• 重复元素下的快排
• 基本有序下数组下的快排

一、快速排序是如何工作的？

个人理解，快速排序的工作原理：每轮任意选定一个支点pivot然后确认其最终的位置，然后对支点两边的进行相同的操作，逐渐靠近直至到达有序状态的过程。因此快速排序是分区+递归，分而治之的。

1.1.分区

可以看出，快速排序的核心在于：分区。即确定选定支点pivot的最终位置。支点的最终位置在哪里？如果支点的最终位置为x，对于数组arr必然满足

1
2
3
4
5
6
7
8
9
10
11
12
13

private int partition(int[] arr, int low, int high) {
    int pivot = low;
    int pivotValue = arr[pivot];
    while (low < high) {
        while (low < high && arr[high] ≥ pivotValue)
            high--;
        while (low < high && arr[low] ≤ pivotValue)
            low++;
        swap(arr,low,high);
    }
    swap(arr,pivot,low);
    return low;
}

1.2.递归

递归对应分而治之中的治。为什么经过快速排序后，数组能够变成有序的？不如先看看代码。

1
2
3
4
5
6
7

public void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        int pivot = partition(arr, low, high);
        quickSort(arr, low, pivot - 1);
        quickSort(arr, pivot + 1, high);
    }
}

读完代码，可以得到以下信息：
1.条件判断是最优先的
2.递归过程类似于二叉树的先序遍历

对于第1点，条件判断先行是为了防止栈溢出或数组越界，没什么好讲的。
对于第2点，递归过程很像二叉树的先序遍历，如下图所示：

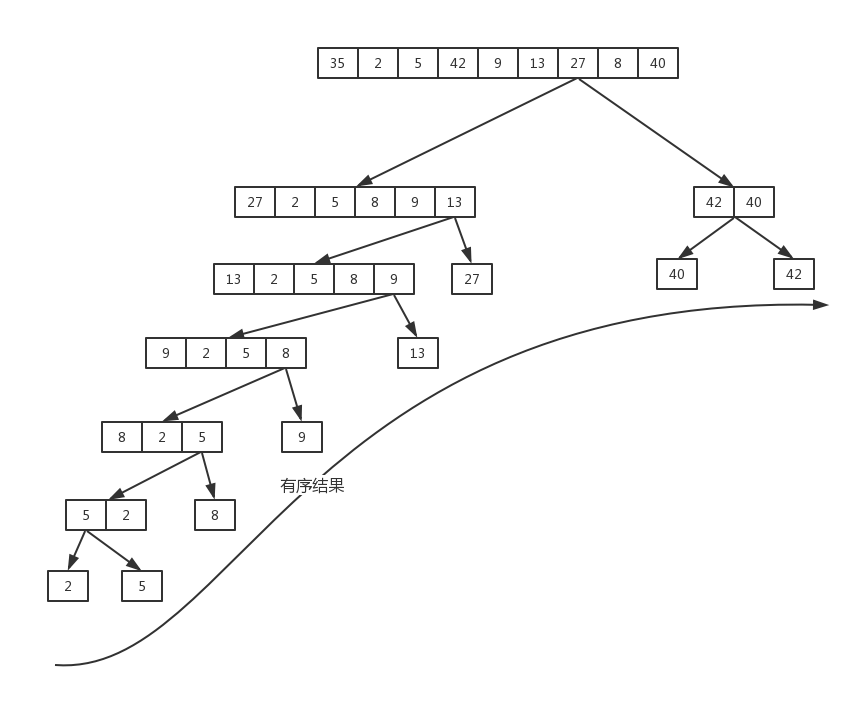
从图中可以看出，如果达到最大递归深度，即low+1=high，图中的叶子节点时会回溯，且每个叶子节点都是有序的，所以所有的叶子节点合起来从左至右是有序的。

1.3.复杂度

快排的时间性能如何？从上面可看出快排的过程类似一个二叉树的遍历，最大递归深度直接决定快排的时间性能。假设待排序数组是完全随机的，设时间频度为T(n)，在平均和最佳的情况下，有
T(n) = 2T(n/2) + n
       ≤ 4T(n/4) + n
       ≤ 8T(n/8) + n
       … …
       ≤ log₂n + nlog₂n

因为待排序数组是完全随机的，所以可以认为，i和j指针移动1，2，3…n次的概率为1/n，因此移动距离的期望为n/2，所以一份T(n)可以分成2个T(n/2)加上扫描一次的代价，且扫描一次的代价必然≤n的。所以平均和最佳的情况下，快排的时间复杂度均为O(nlog₂n)。
同时，在最佳的情况下，T(n)同样也是被一分为二的，两份的大小相等，因此和平均的情况一样。

在最差的情况下，即数组完全有序，快排的时间性能直接退化到O(n²)，相当于冒泡排序，递归树退化成链表。

二、重复元素下的快速排序

重复元素较多下的快排递归树:

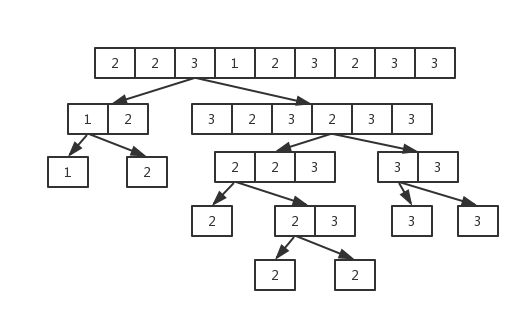
从图中来看，似乎并没有什么问题，递归树还算比较平衡。但是，数组中共有4个2，4个3，但是普通的快速排序为每个2和每个3都分别确定他们的最终位置，这样的操作显然重复了。如何去掉这些重复操作？可以用三路划分的快速排序。
在上图中，数组中共有4个2，4个3，如果能一次确定2或3的最终位置就好了。答案是可以的。在经过一次分区后，我们希望arr[low…high]是这样的

数组的每个元素和pivotValue的大小关系从左到右是<，==和>的，==pivotValue的部分的长度可能不为1。问题是如何达到这个状态。我们可以从五路划分开始，如下图：

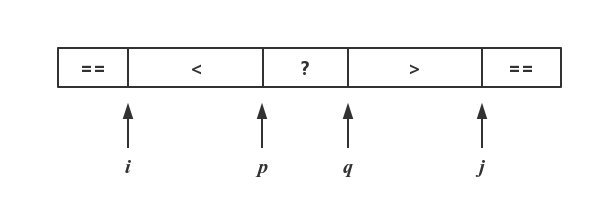
为什么可以使用五路划分？或者说，是怎么想到先五路划分的？首先，我们需要明白，在快速排序的分区过程中：

• 左右指针没有相遇前，pivotValue的最终位置无法确定
• 分区函数的目的是确定pivotValue最终的位置

在左右指针没有相遇前，最终位置是无法确定的。我们的目标是划分三路，但是能够划分三路的前提是，我们知道了pivotValue的最终位置。在不知道最终位置之前，我们必须找到一个空间来暂时存储和pivotValue的值。最简单的思路是再开辟一个辅助空间。然而快速排序的最大优势是原地排序+nlog₂n的时间复杂度，如果另外开辟空间，就不再是原地排序，有点舍本取末。因此，还是尽量的不开辟新空间。这是暂时想不出空间复杂度O(1)的缓存方案，不如从第二点入手：分区函数是确认pivotValue最终的位置。就像上面1.1.所说的，这个位置的值是pivotValue。或者说，只要保证最终位置的值是pivotValue就行了，至于其他位置的值是多少可以不用管。因此，其他位置的数据在不损失的条件下是可以操作的，也就是说可以交换。因此，缓存方案就出来了：随机区域的左边，如果遇上和pivotValue相等的值，那就将其放置在表头；随机区域的右边，如果遇上和pivotValue相等的值，就将其放在表尾。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

while (p < q) {
    while (p < q && arr[q] >= pivotValue) {
        if (arr[q] == pivotValue) {
            swap(arr, j, q);
            j--;
        }
        q--;
    }
    while (p < q && arr[p] <= pivotValue) {
        if (arr[p] == pivotValue) {
            swap(arr, i, p);
            i++;
        }
        p++;
    }
    swap(arr, p, q);
}

if (arr[p] == pivotValue) {
    p--;
    q++;
}

需要注意的是退出循环后p == q，arr[p]和pivotValue的大小关系是不能确定的。如果arr[p] == pivotValue，那p--一次，q++一次就OK了。否则不做任何操作，这是为五路化为三路打好基础。
因此这份代码结束后，arr可能是两种情况：

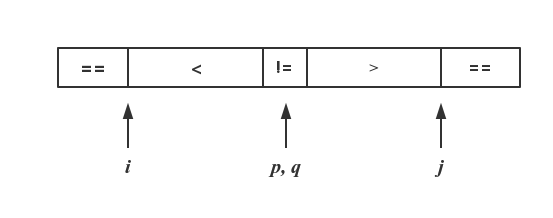
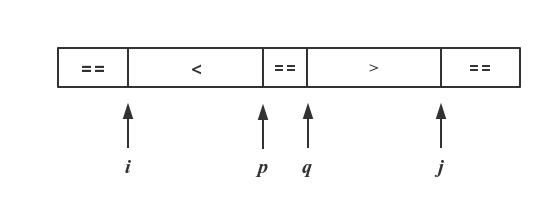
第一张图代表arr[p] != pivotValue 的情况，此时p，q指针不必移动；
第二张图代表arr[p] == pivotValue 的情况，此时p，q指针分别需递减和递增一次。

因为表头表尾都是和pivotValue相等的值，而且pivotValue的最终位置已经确认(p所指向的位置)，所以可以：

• i，p指针所指向的位置交换，同时一起递减，直至i ≥ low
• j，q指针所指向的位置交换，同时一起递增，直至j ≤ high

所以代码出来了

1
2
3
4
5
6
7
8
9
10

while (i > low) {
    swap(arr, i - 1, p);
    p--;
    i--;
}
while (j < high) {
    swap(arr, j + 1, q);
    q++;
    j++;
}

需要注意一点的是，在交换的时候，i(j)需要减(加)1，这是因为：在发现和pivotValue相等的元素时，是和i(j)的位置交换后，在i++(j--)的，因此i(j)和等于pivotValue的位置是错开一格的，因此i(j)需要减(加)1。

此时就能从五路转化成三路。此时arr[p…q]都等于pivotValue。
完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

private int[] partition3(int[] arr, int low, int high) {
    int i = low;
    int j = high;
    int p = low;
    int q = high;
    int pivotValue = arr[low];
    while (p < q) {
        while (p < q && arr[q] >= pivotValue) {
            if (arr[q] == pivotValue) {
                swap(arr, j, q);
                j--;
            }
            q--;
        }
        while (p < q && arr[p] <= pivotValue) {
            if (arr[p] == pivotValue) {
                swap(arr, i, p);
                i++;
            }
            p++;
        }
        swap(arr, p, q);
    }
    if (arr[p] == pivotValue) {
        p--;
        q++;
    }
    while (i > low) {
        swap(arr, i - 1, p);
        p--;
        i--;
    }
    while (j < high) {
        swap(arr, j + 1, q);
        q++;
        j++;
    }
    return new int[]{p + 1, q - 1};
}

还是要啰嗦一下，因为边界条件非常重要：最后返回的时候返回的是「new int[]{p + 1, q - 1}」，p(q)是加(减)1后返回的。因为在最后五路归三路的时候，是先交换在p--(q++)的。因此会错开一位，道理跟上面的i(j)是一样的。

三、基本有序下数组下的快排

还是从快排的核心——分区函数入手。在完全有序的情况下，时间频度T(n)为：
T(n) = T(n -1) + T(1)
       = T(n -2) + 2 * T(1) + n
       = T(n -3) + 3 * T(1) + n + (n - 1)
       … …
       = T(1) + (n - 1) * T(1) + n + (n - 1) + … + 2
       = n * T(1) + n + (n - 1) + … + 2 + 1
       = n * T(1) + n²/2 + n/2
因此，在基本有序的情况下，时间频度T(n)是接近于n * T(1) + n²/2 + n/2(T(1)为常数)的。此时递归树极度不平衡。
因此在基本有序的数组下，快速排序的性能是十分差的。因此，在数据基本有序的情况下，使用插入排序更好。
顺便提一下，插入排序的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public void insertSort(int[] arr) {
    int i;
    int j;
    for (i = 1; i < arr.length; i++) {
        if (arr[i - 1] > arr[i]) {
            int t = arr[i];
            arr[i] = arr[i - 1];
            for (j = i - 1; t < arr[j]; j--) {
                arr[j + 1] = arr[j];
            }
            arr[j + 1] = t;
        }
    }
}

当数据基本有序时，可以近似认为，插入排序只是把待排数据扫描一遍而已。

四、总结

快速排序是一个时间复杂度为O(nlog₂n)的原地排序。它是的基本原理是确认每轮任意选定一个支点pivot的最终的位置，然后对支点两边的进行相同的操作，逐渐靠近直至到达有序状态。数组应当随机顺序，这样才能保证快速排序的最佳性能，否则可以考虑使用插入排序。倘若遇到重复率较高的随机顺序数组，可以考虑使用三路划分的快速排序来提升排序速度。

五、感想

因为之前有简单了研究过，所以这篇文章写的很快，一天就出来了。之前研究的时候，发现快速排序简洁代码的背后蕴含着很多信息，教材给出的代码也只适用于pivot=low的情况，后来我改进了一下，pivot可以任意选，然后就顺手实验一下不同的pivot对快速排序的时间性能影响。通过研究快速排序的机会，我知道了对于排序算法，边界条件很重要，否则很有可能造成数组越界，在递归的情况下也可能造成栈溢出。还有就是任何算法都要在草稿纸上写写画画，这样才能更容易理解其中的原理。

• ← Previous Post
• Next Post →